Continuity of a Function
Continuity of a Function: Overview
This topic covers concepts such as Continuity of a Function, Continuity of a Function at a Point, Continuity in an Interval, Discontinuity of a Function, Reasons for Discontinuity of a Function at a Point, Infinite Discontinuity, etc.
Important Questions on Continuity of a Function
Let be a polynomial of degree one and be a continuous and differentiable function defined by . If , then
Choose the correct statement on the continuity of the function given by at
Choose the correct comment explaining the continuity of the function f defined by
If is continuous at then
Let f be a real-valued function defined on the interval by Then which of the following statement(s) is (are) true?
Function has oscillatory discontinuity at point .
Function has oscillatory discontinuity at point .
Define the oscillatory discontinuity with one example.
This is the graph of a function .
Find the -value at which has a jump discontinuity.
Define infinite type of non-removable discontinuity with one example.
Define isolated point discontinuity with one example.
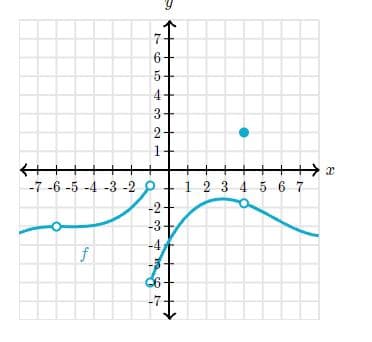
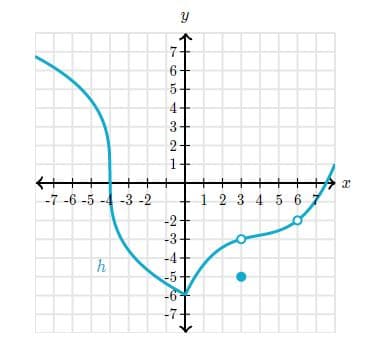
This is the graph of a function .
Find the -value at which has an isolated point discontinuity.
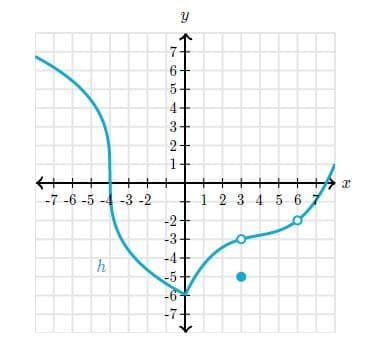
This is the graph of a function .
Find the -value at which has a isolated point discontinuity.
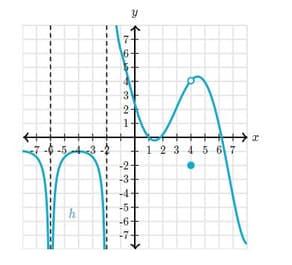
This is the graph of a function . Dashed lines represent asymptotes.
Select the -value at which has an isolated point discontinuity.
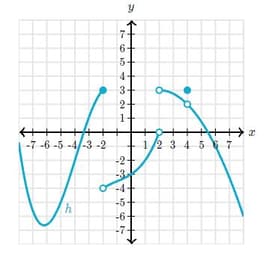
This is the graph of a function .
Find the -value at which has a isolated point discontinuity.
This is the graph of a function .
Find the -value at which has a missing point discontinuity.
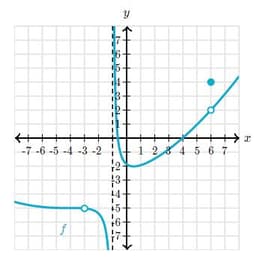
This is the graph of a function . Dashed lines represent asymptotes.
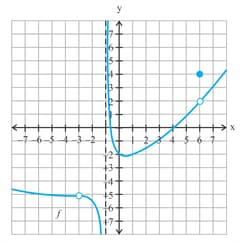
Select the -value at which has a missing point discontinuity.
Let function .
The function has a missing point discontinuity at .